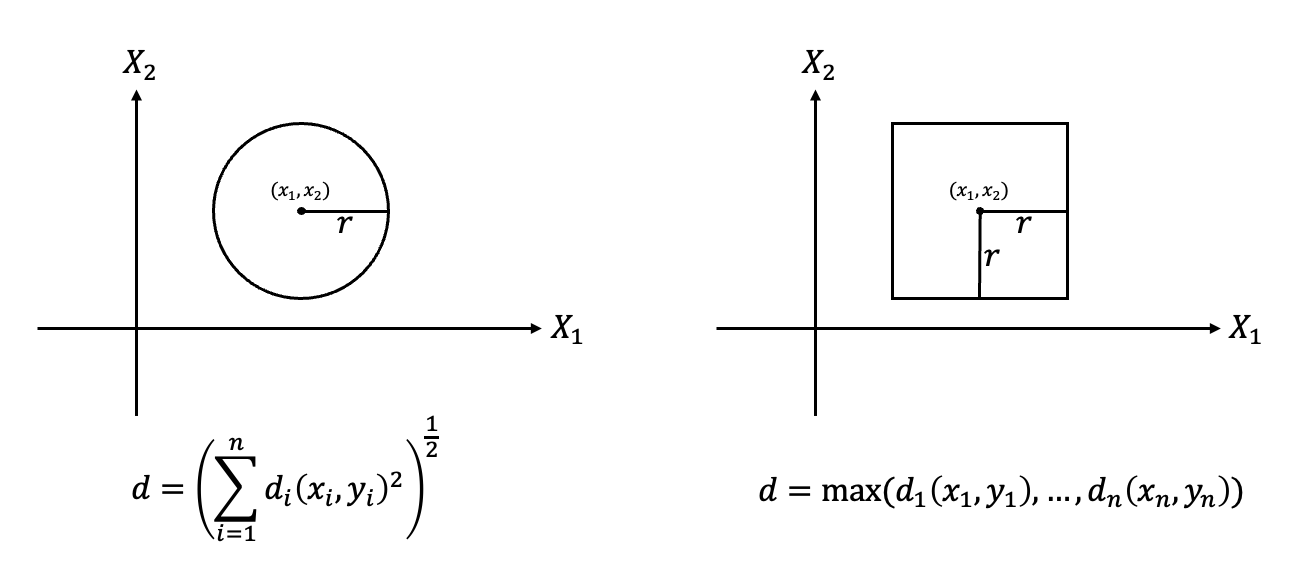Products of Metric Spaces
여러 개의 Metric space (X1,d1),...,(Xn,dn) 이 있을 때 이들의 곱으로 새로운 Metric Space를 정의할 수 있다.
Product set X=X1×⋯×Xn 은 조합 가능한 모든 n-tuple (x1,...,xn) 으로 이루어지고, 이에 적절한 metric을 정의해주면 X 는 Metric Space가 된다.
예를 들어 x=(x1,...,xn),y=(y1,...,yn) 에 대해 d(x,y)=[∑i=1ndi(xi,yi)2]1/2 와 같이 정의하면 d 는 metric의 정의를 만족한다.
정의만 만족한다면 얼마든지 metric을 정의할 수 있다. d(x,y)=max(d1(x1,y1),...,dn(xn,yn)) 역시 metric이 될 수 있다. (이를 보이는 것은 연습문제)
위의 두 metric이 각각 X=R×R 에 적용된다면, 이 Metric Space에서 open ball의 모습은 다음과 같게 된다.
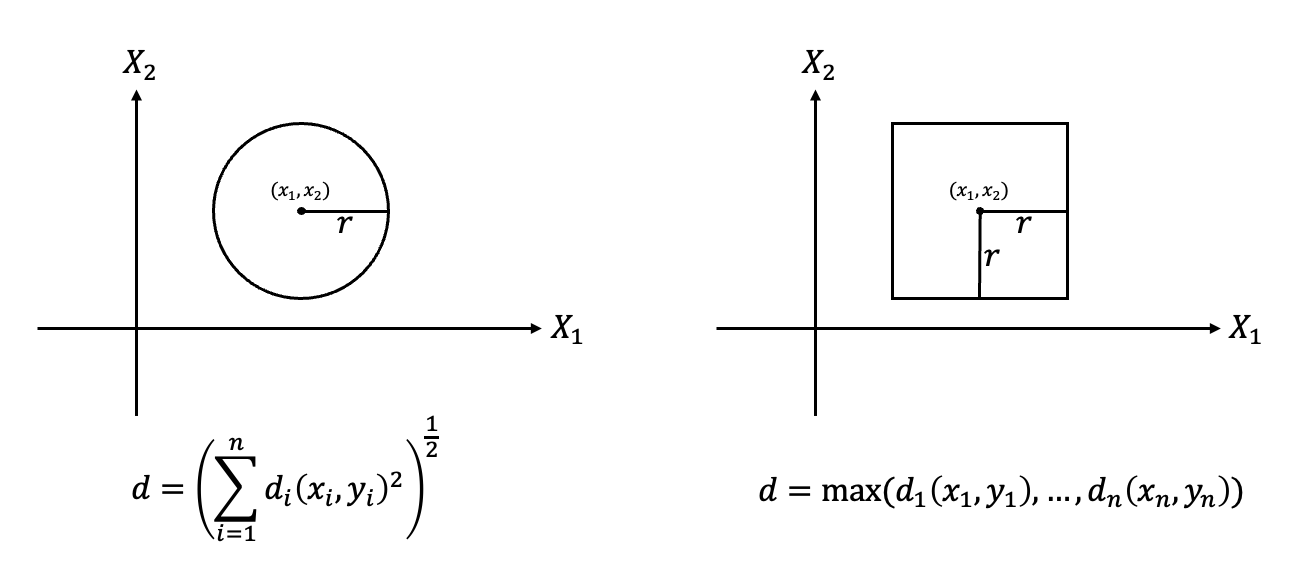
Theorems
이와 관련된 정리로, 특정 조건을 만족하는 metric이 적용된 Metric space에 대해 다음이 성립한다.
- X=X1×⋯×Xn 와 이에 대한 metric d 로 이루어진 Metric Space (X,d) 의 open set은, U1×⋯×Un 와 같은 형태의 product set들의 union으로 표현할 수 있다.
(Ui 는 Xi 의 open set, 1≤i≤n)
- Metric Space (X1,d1),...,(Xn,dn) 각각이 모두 complete하면, X=X1×⋯×Xn 와 이에 대한 metric d 로 이루어진 Metric Space (X,d) 또한 complete하다.
2025.07.30
References
Introduction to Topology, 2ed (T.W. Gamelin and R.E. Greene)